Binary Index Tree
Orion Electric Age
  2020-01-10 21:23:01 2020-01-10 21:23    

Binary Index Tree

Binary Indexed Tree also called Fenwick Tree provides a way to represent an array of numbers in an array, allowing prefix sums to be calculated efficiently. For example, an array [2, 3, -1, 0, 6] is given, then the prefix sum of first 3 elements [2, 3, -1] is 2 + 3 + -1 = 4. Calculating prefix sum efficiently is useful in various scenarios. Let’s start with a simple problem.

Problem:
Description of GCD Sum
Function F is defined as,
F(x) = GCD(1,x) + GCD(2,x) + ... + GCD(x,x)
where GCD is the Greatest Common Divisor.

Given an array A of size N, there are 2 types of queries:
1. C X Y : Compute the value of (F(A[X]) + F(A[X+1]) + F(A[X+2]) + ... + F(A[Y])) (mod(10^9 + 7))
2. U X Y: Update the element of array A[X] = Y

Input:
First line of input contains integer N, size of the array.
Next line contains N space separated integers the elements of A.
Next line contains integer Q, number of queries.
Next Q lines contains one of the two queries.

Output:
For each of the first type of query, output the required sum mod(10^9 + 7).

Constraints:
1<=N<=10^6
1<=Q<=10^5
1<=A[i]<=5*10^5

For update,
1<=X<=N
1<=Y<5*10^5

For compute,
1<=X<=Y<=N

SAMPLE INTPU:
3
3 4 3
6
C 1 2
C 1 3
C 3 3
U 1 4
C 1 3
C 1 2

SAMPLE OUTPUT:
13
18
5
21
16

Binarty Index Tree Layout

//for ease, we make sure our given array is 1-based indexed
int a[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};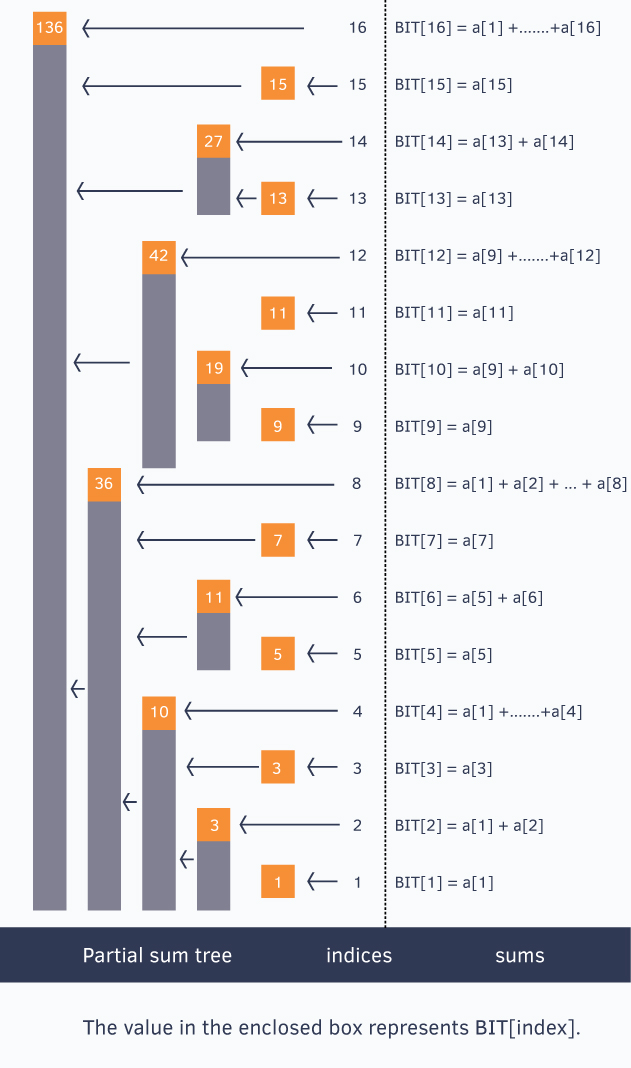
Binary Index Tree Layout

Code Implementation

  • Main

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    #include <stdio.h>
    #include <stdint.h>

    #define V_MAX (500000 + 1)
    #define MOD_BASE (1000000000 + 7)

    //#define DBG(f_, ...) do { printf((f_), ##__VA_ARGS__); } while(0)
    #define DBG(f_, ...)

    int main()
    {
        int *arr;
        long long *BIT;
        int i, size, opts, value;
        long long phi[V_MAX], sums[V_MAX];
        char opt;
        int x, y;
        
        scanf("%d\n", &size);
        arr = malloc(sizeof(int) * (size + 1));
        if (!arr) {
            return 0;
        }
        BIT = malloc(sizeof(long long) * (size + 1));
        if (!BIT) {
            free(arr);
            return 0;
        }
        memset(arr, 0, sizeof(int) * (size + 1));
        memset(BIT, 0, sizeof(int) * (size + 1));
        
        memset(phi, 0, sizeof(phi));
        memset(sums, 0, sizeof(sums));
        SumOfGCDs(sums, phi, V_MAX);
        
        DBG("Array size %d\n", size);
        i = 0;
        while ((++i) <= size && (scanf("%d", &value) != EOF)) {
            if (value >= V_MAX) {
                continue;
            }

            arr[i] = sums[value];
            Update(BIT, i, arr[i], size);
            
            DBG("arr[%d] = %d, gcdsum=%d\n", i, value, arr[i]);
        }
        
        scanf("%d\n", &opts);
        DBG("Options %d\n", opts);
        i = 0;
        while ((++i) <= opts && (scanf("%c %d %d\n", &opt, &x, &y) != EOF)) {
            int nValue;
            
            DBG("Opt: %c %d %d\n", opt, x, y);
            switch (opt) {
                case 'C':
                    printf("%d\n", (Query(BIT, y) - Query(BIT, x - 1)) % MOD_BASE);
                    break;
                case 'U':
                    nValue = sums[y];
                    Update(BIT, x, -arr[x], size);
                    Update(BIT, x, nValue, size);
                    arr[x] = nValue;
                    break;
            }
        }
        
        free(arr);
        free(BIT);
        
        return 0;
    }

  • Construct&Update

    1
    2
    3
    4
    5
    6
    void Update(long long *BIT, int idx, long long diff, int n)
    {
        for (; idx <= n; idx += (idx & (-idx))) {
            BIT[idx] += diff;
        }
    }

  • Query

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    long long Query(long long *BIT, int idx)
    {
        long long sum = 0;
        
        for (; idx > 0; idx -= (idx & (-idx))) {
            sum += BIT[idx];
        }
        
        return sum;
    }

  • Euler’s Totient function

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    // Precomputation of phi[] numbers. Refer below link 
    // for details : https://goo.gl/LUqdtY 
    void ComputeTotient(long long *phi, int size) 
    {
        int i, j;
        
        // Refer https://goo.gl/LUqdtY 
        phi[1] = 1; 
        for (i = 2; i < size; i++) {
            if (!phi[i]) {
                phi[i] = i - 1; 
                
                for (j = (i << 1); j < size; j += i) {
                    if (!phi[j])
                        phi[j] = j;
      
                    phi[j] = (phi[j]/i) * (i - 1);
                }
            }
        }
    }

    void SumOfGCDs(long long *sums, long long *phi, int size)
    {
        int i, j, k;
        
        ComputeTotient(phi, size);
        
        for (i = 1; i < size; i++) {
            // Iterate throght all the divisors 
            // of i. 
            for (j = i, k = 1; j < size; j += i, k++) {
                sums[j] += (i*phi[k]);
            }
        }
    }

  • Cautions

– sum overflow, so with long long
– index 0 is ommited of BIT array

Reference